Time & Space Complexity

Time Complexity

Big-O , Big-Omega , Big-Theta

  • Big-O is the upper asymptotic bound for an algorithm . Worst-case scenarios
  • Big-Omega is the lower bound asymptotic bound of an algorithm. Bast-case sceanrio
  • Big-Theta is in between lower and upper asymptotic bound (tight bound) of an algorithm. Average or expected case scenario

Space Complexity

Amount of memory or space required by an algorithm

In recursive calls counts,the code would take 0 (n) time and O( n) space.

int sum(int n) { 
if (n <= a) {
return B;
 }
 return n + sum(n-1);
 }

Each call adds a level to the stack.

  • sum(4)

    • sum(3)

      • sum(2)

        • sum(l)

          • sum(0)

Each of these calls is added to the call stack and takes up actual memory.

A few tips

  • Drop the non-dominant terms

1. O(W + N) becomes O(W)
2. O(N + log N) becomes O(N)
3. 0(5*2N + 1000N^100 ) becomes O(2N)

  • Multi-part algorithms - Add vs Multiply

  • Amortized time

    • An ArrayList or a dynamically resizing array, allows the benefits of array + resizing
    • Array has finite size while arrayList have flixbility in size.

The array could be full. Suppose an array contains N elements, then inserting a new element will take 0 (N) time. We need to create a new array of size 2N and then copy N elements over. This insertion will take 0 (N) time. This insertion wont happen time and again , however it(insertion) would take O(1) time. This is the time where we say time is “Amortized”

  • Log N Runtimes

Lets take example of Binary search. We first compare x to the midpoint of the array.

  • If x == middle, then we return 1
  • If x < middle, then we search on the left side of the array.
  • If x > middle, then we search on the right side ofthe array.

In this way , if we observe - we are stepping down n/2 elements , then n/4 and then n/8 ,etc.

This is how we reach to O(log N) time complexity. It is nicely explained in CTCI book - Please have the book - it has really good content.

  • Recursive functions

Example of Fibonacci series using recursive function

int f(int n) {
 if (n <= 1) {
 return 1;
 }
 return f(n - 1) + f(n - 1);

Lets consider how the calls of above code in tree stack

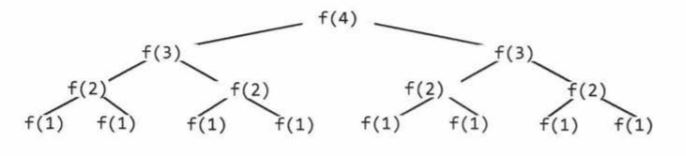
For each level and node , lets compute the number of calls

Note : O( branches^depth ) for most of recursive functions.

This is the reason why Recursive calls are very expensive.

Pic credit : CTCI (Big O chapter)

Examples from CTCI Book

CTCI - Excellent book - here

Example 1

Time Complexity = O(N)

Example 2

Time Complexity = O(N^2)

Example 3

Time Complexity = O(N^2)

Example 4

Time Complexity = O(ab)

Note : There are 2 different arrays (a and b) in the nested loop